When programming systems it makes sense to keep complexity and scale in mind. Don’t try and render 400,000 sprites all at once. Don’t try and send the entire world state to every player on the server. What about our design tools, though? Are we being too cautious when it comes to coding, and what riches might we be able to access if we jumped in the deep end from time to time? This week on Reading The Papers: the power (and responsibility) of computing everything at once.
We’re reading An Argument for Large-Scale Breadth-First Search for Game Design and Content Generation via a Case Study of Fling! by Nathan Sturtevant. In it, Nathan describes a system he built for exploring the mechanics and levels of an iOS puzzle game called Fling! Unlike most tools that might be used for solving or assisting in the design of puzzles, Nathan’s approach uses brute force search and parallelisation to explore the space of possible puzzles. He raises some intriguing points about brute force approaches and their application to procedural content generation – something I think could be really relevant to a lot of developers right now.
Let’s start by talking about Fling! The screenshot above is from the game – an 7×8 grid on which balls are placed. You can swipe a ball in a direction, and it will move until it collides with another ball, which will be pushed in that direction while the original ball stops moving. The objective is to push all but one of the balls off the screen. In the game the number of balls in a single level goes as high as 14, but as Nathan points out this is a fairly arbitrary limit. In theory, there are over 5.8 trillion potential ways of arranging balls on that 7×8 grid – just storing a single bit to record if each level was solvable would take 675GB of space. Of course, we’re not interested in all of the possible combinations, just ones which are solvable. Still, that must be a huge number, right?
Beginning at boards with just one ball in (all of which are successful game states by definition) Nathan wrote a program that built up a database of solvable Fling! levels. In order to generate solvable levels containing n balls, you can start with all solvable levels containing (n-1) balls and add a single extra piece to them, then check if they can be reduced to solvable levels in a single move. This elegant bit of calculation means that Nathan’s code took just two hours to calculate all solvable levels of 10 pieces or less – faster than it took to write the code in the first place, as he points out. This forms an endgame database, which is a key part of the tool described in the remainder of the paper.
By loading the endgame database directly into memory (the work described in this paper uses the 9-piece database for speed, but there’s no reason why larger numbers of pieces wouldn’t work) Nathan was able to develop a tool that could represent Fling! game states and then answer the following questions:
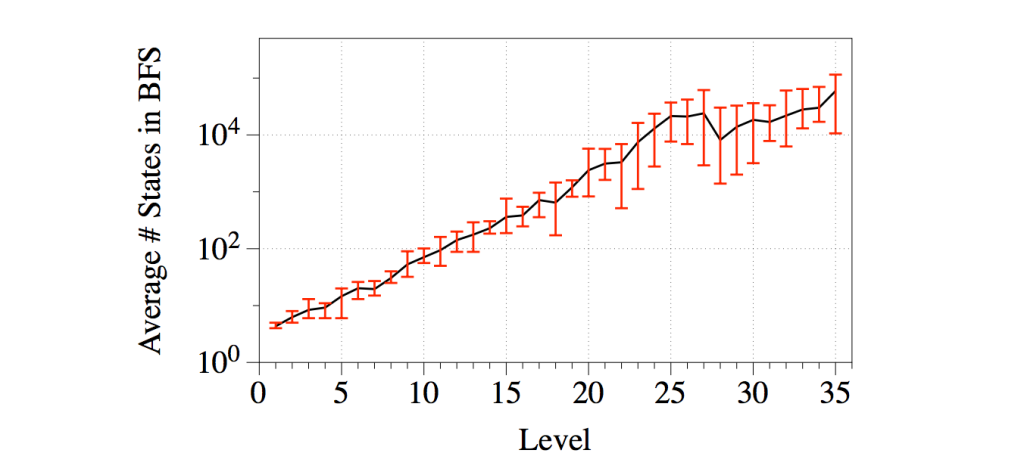
- How many states can I reach from this game state? That is, how many different moves can I make in total in this level, exploring all the way through to all failed and success states. We’ll come onto why this is useful later, but this can be a big number as the levels get bigger.
- How many starting moves lead to a solution? This can be calculated with help from the endgame database. The tool annotates the level with little white arrows showing these starting moves – incredibly helpful for a designer wanting to visualise the solution space.
- What effect would single changes have on the board? When you present a Fling! level to the tool, it checks each of the 56 tiles on the board and either adds or removes a ball to it, then rechecks the board. Using this data, it can shade tiles that would either make a solvable level unsolvable if it were changed, or vice versa.
What you end up with is a tool that can show you how many potential starting moves a puzzle has, how to fix (or break) a puzzle, and also tell you how big this puzzle is in terms of possible moves. Why is that last point a big deal? Here’s a graph showing the level number (on the X-axis) versus the total number of states (on the Y-axis, logarithmic) in the original Fling! game:
In other words, the number of states in this level’s search tree seems very closely related to what the game’s designer thought of as difficulty. Which makes sense – the more wrong alleys there are to go down, the more potential there is for a player to trip up. What if they aren’t all wrong alleys? Nathan’s already ahead of you there. By analysing Fling!’s levels, he found that every level was designed to have a single valid solution path. That is, there is only ever one right move to make on the board (Nathan tells me there are some interesting conclusions you can draw from this about certain kinds of moves, given that there’s only ever one correct move – he’s looking into these at the moment).
What’s important to take away here is that both the endgame database and the tool’s analysis of level designs is done more or less exhaustively – there are no search heuristics guiding the tool towards finding levels it’s been told might be good, or moves it’s been told might be productive. Instead, it searches all possible moves, it explores all possible routes through the search space, and as a result you find that actually that space wasn’t so scary after all. And once you have that complete archive of every possible level in memory, a human designer can sit down and really get to grips with a level design.
You might think that this is all well and good for grid-based games with small state spaces. And it absolutely is. There are plenty of people working on incredible grid-based games with small state spaces, and even when that state space increases just a little bit we may still find it tractable to store endgame databases and exhaustively explore the design space.
All the work described in the paper uses parallel processing wherever it can, since individual game states are unrelated to each other (there’s no data to bear in mind like health). Even this could be added to the state representation rather than holding it in data. A game like Corrypt has very few resources – each level could be processed a few times with differing resource levels embedded in the game state.
The real importance of the paper is not the specific problem the tool solves, though. It’s the rewards that Nathan found by attempting to exhaustively solve a problem instead of tiptoeing through it with the usual applications of A* search and optimisation techniques. Vast memory reserves, multithreading, cloud computing – we have a lot of resources at our fingertips these days, and that should make us reconsider the use of brute force techniques. What was once a one-way ticket to slowdown and memory overflows could now be a powerful new way of looking at game design.
Where To Find More
Nathan is currently an Assistant Professor at the University of Denver. He presented this work in a fantastic talk at the AI in the Design Process workshop at AIIDE 2013, and really impressed me with the results in the paper. I hope I got some of it across! Do get in touch with him if you want to talk more. If you’re at the AI Summit at GDC this year, Nathan will be talking about Monte Carlo search – he’s a great speaker who’s done a terrifying wealth of work on search techniques, so I recommend checking the talk out! If you’re interested in the work in relation to Fling! then apparently Nathan’s working on a new level pack for Fling! based on some of the ideas this tool started from, and mixing in some automated design as well. I’m really excited to see more about this – perhaps another Reading The Papers in the future…
As ever, you can get in touch with me via Twitter with feedback on this week’s column. Ludum Dare results next week – don’t forget to check in at my site for updates on how ANGELINA performed in its very first game jam.